Category Archives: ProTrader

Jason Alt, ProTrader, Unlocked ProTrader

UNLOCKED PROTRADER: Digging for Gold

On a recent episode of the Money Draught podcast, financier JR (@time_elemental) lamented the lack of real EDH cards in Modern Masters 2015. While Modern Masters…One (I guess) included a lot of EDH staples in an attempt to bring their prices down while simultaneously not acknowledging the secondary market, Modern Masters 2015 doesn’t seem to.

Not only that, the cards that are included aren’t quite build-arounds like last time. While Doubling Season was the linchpin in a draft archetype, we don’t see similar things in Modern Masters 2015. The lack of real EDH cards is going to confound our ability to predict what prices will do to an extent, but let’s dive in anyway. Even though we don’t have a ton of EDH cards this time, there is some gold there.

So what exactly did we get handed to us last time?

Wow, that’s quite a list. We had a substantial portion of the set overlap with cards we find useful in EDH. Let’s compare the size of the list to the size of the list from Modern Masters 2015.

If some of those are a bit of a stretch, don’t worry, because even with me stretching the list out, it’s much, much shorter than the list of EDH goodies in the first Modern Masters set.

With Modern Masters 2015 promising an even larger print run than the first Modern Masters set, expect prices to dip even more profoundly than last time even after you account for all the product that is going to be damaged by WOTC’s shoddy, experimental packaging.

How much do we expect to see prices dip? When should we buy in for some of these cards? Which cards’ prices do we never expect to recover? What are some factors that we don’t always consider? Let’s delve in a bit and see if we can’t make a few predictions based on last time, where we saw a smaller print run but also way more people excited to open boosters.

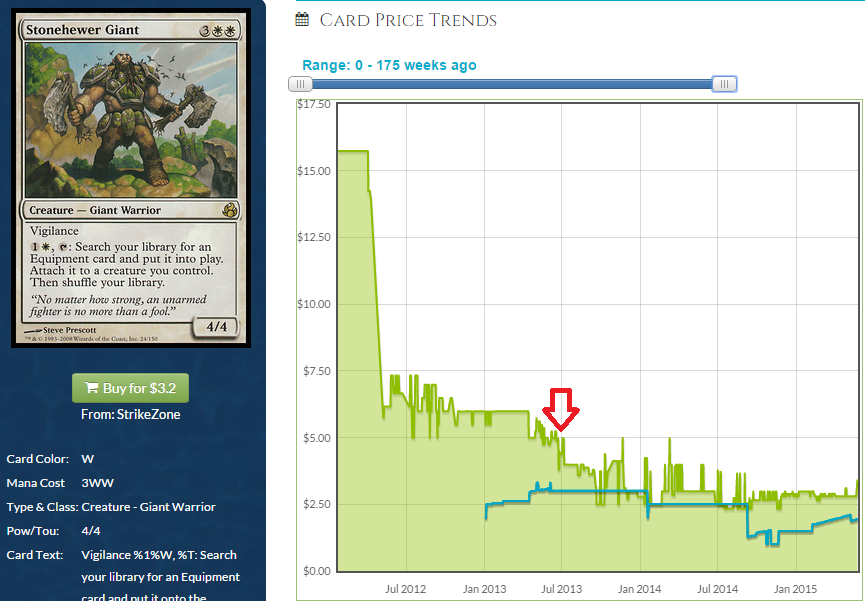
Untitled

Reality had a profound effect on the price of Stonehewer, bringing it down to the $5 range long before the announcement of the reprint, but Modern Masters took a solid EDH staple that most valued as a bulk rare without knowing it was a solid $5 pick and turned it into a card worth half that at best. Even the printing of a mono-white, equipment-themed EDH deck only affected the spread—it increased slightly but the price is thus far unperturbed two years on. Stonehewer demonstrated an ability to be in high demand and fetch ridiculous prices when everyone was equipment crazy, but if that happens again, don’t expect Giant to be able to reach its previous ceiling. It’s possible its price of above $10 may have prompted its inclusion in Modern Masters, since it took so long for the set to go from conception to boosters, but regardless, we’re only seeing faint glimmers of price recovery two years on.

You can sort of control for the effect of Modern caring less about Giant if you look at another card touted in Modern initially and abandoned at the same time: Steelshaper’s Gift. If you look at the price of Steelshaper’s Gift over the same time frame as Giant, the effect of Modern becomes clearer and you can see what was that demand decrease and what was purely the result of the reprinting in the first Modern Masters set. This isn’t exactly a quantitative effect, but even a qualitative one can show there are two distinct periods of price decline and which one was predicated on the reprint.

Do I see a corollary in Modern Masters 2015?

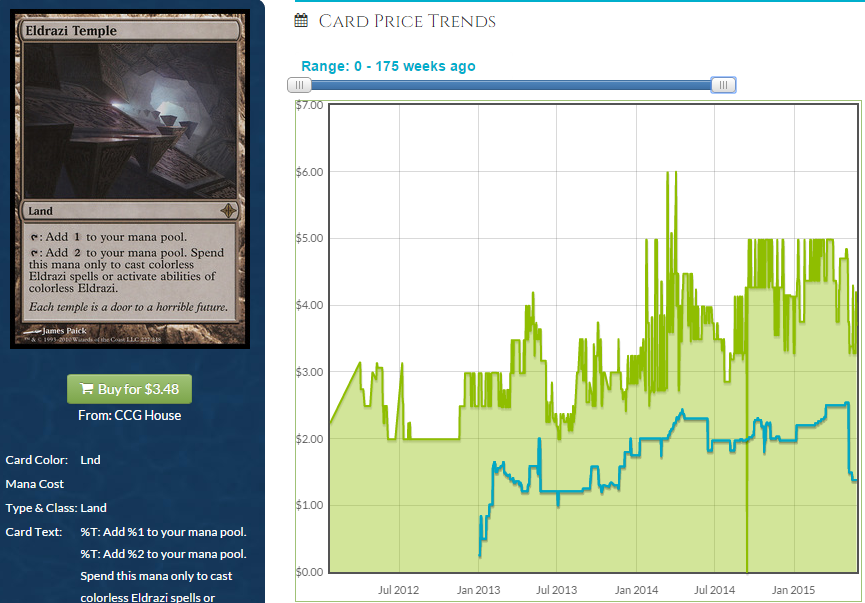
Untitled

While we don’t expect ordinary cards in the $5 range to recover in price, expect Temple to be crushed into powder. A reprint at uncommon is going to be devastating to the price, and the spread reflects that: growing astronomically as dealers head for the hills.  While its price isn’t predicated on EDH play, I see this card and it’s $5-ish price tag and think of Stonehewer’s abject failure to recover its price despite there being more excitement around a card like it than ever before. Narrow cards like Stonehewer that are good at what they do but relegated to only a few decks are going to suffer for longer than the two years it has been since the last Modern Masters set, and I expect Eldrazi Temple is entirely done for as a result. While some uncommons like Path to Exile have demonstrated an ability to stay around $5, Eldrazi Temple is not Path, and a realistic floor could end up under $1. If it had been reprinted at rare, I’d still expect it to hit $2.

How does this compare to a card reprinted in a different manner? Let’a look at an EDH staple that was reprinted in a Commander deck and see if we see a similar price decline or a dissimilar one. Since we are decent at predicting what a Commander reprint will do, let’s try and compare the two effects and try to apply that to a card in Modern Masters 2015.

62553954

Murkfiend Liege is a great, great card. It’s a fairer Prophet of Kruphix and despite being outclassed by the less fair prophet, the community has adopted a, “Por que no los dos?” attitude, so Prophet hasn’t really hurt Liege’s price a ton, especially not compared to what the Commander 2013 reprint did to absolutely pants it.

If you look at this graph of Murkfriend Liege’s price for the Eventide copy, it was well on its way to $15 when the reprint came along and pulled its pants down. The card is dirt cheap right now,but it’s not done going down and I’m not even close to wanting to touch these right now. With the popularity of Derevi, the sealed product is going to continue to be in high demand and every deck popped for a Derevi is going to result in one more Liege hitting the market. Some Derevi players will run the Liege, but some won’t. And besides, that’s a person buying a Seedborn Muse or Prophet (or both) from you who doesn’t need to buy a Liege.

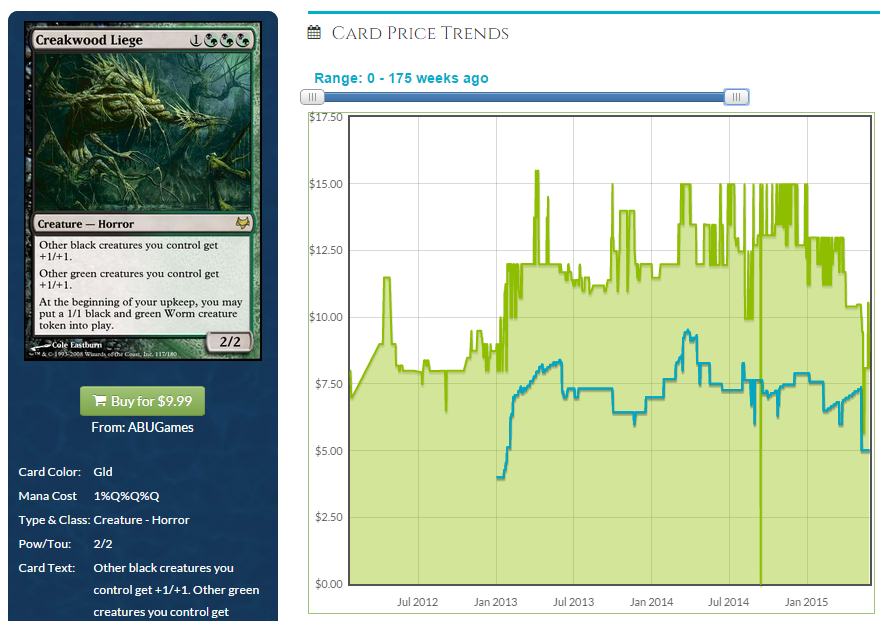
We saw Modern Masters completely pants a card like Stonehewer which was roughly $5 to $7 on EDH demand alone. What about a card that was a similar price to Murkfiend Liege? How about Creakwood Liege?

creakwoodgraph

You can see that the set has already made Creakwood fall to roughly half of its pre-printing price. The good thing is that we can wait for it to fall a bit more, and I don’t know that we’re in any hurry to buy. A reprinting in a Commander deck seems very unlikely. With Modern Masters cutting prices in half last time, I feel like Creakwood Liege may be close to done falling, and this may be the new price for a while, but with Modern Masters threatening to disappear after a few months, it might rebound. Demand was much greater than that for a card like Stonehewer, and with a reprint feeling relatively unlikely after the first one, Liege may recover after all. Can we substantiate our claim that a Modern Masters reprint tends to cut the price of in-demand cards roughly in half?

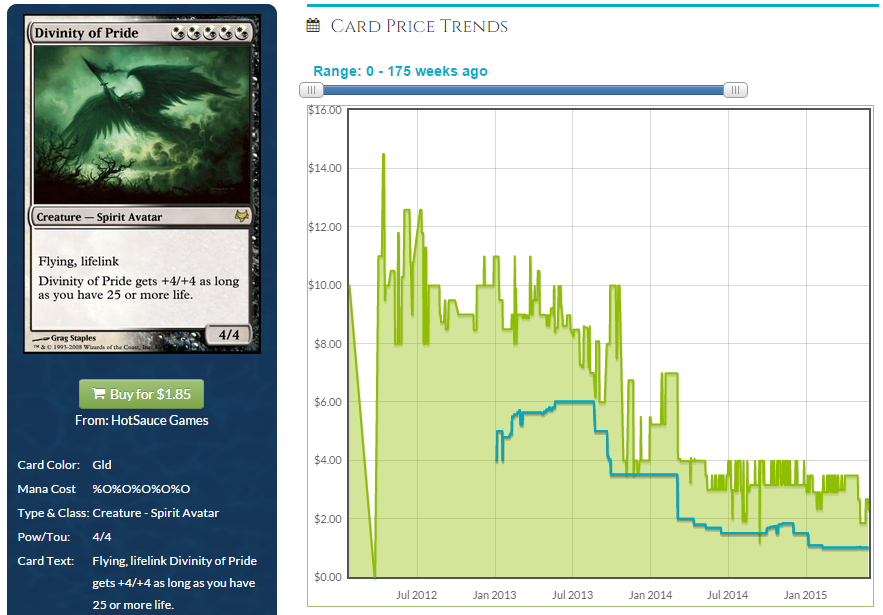
divinityofpridegraph

Divinity has been printed twice and is unlikely to ever recover at a fast enough rate for us to care. You can see two very distinct depressions in price, one around mid-2013 when Modern Masters gave it its first reprinting (cutting the price roughly in half) and the second when it got a reprinting in the Oloro Commander deck which saw some popularity, especially with everyone testing Toxic Deluge at the time trying to deal with True-Name Nemesis.

If we hadn’t seen the second reprinting, Divinity might also have recovered, We can’t say for certain. Do you feel good about Creakwood? If you bought in at its floor, which I would predict is around peak saturation of Modern Masters 2015, you could see it finish between its initial $15 and its current $7.50. That’s a 50 percent increase and would mean it outperformed my 401k. Not too shabby. If you’re not as optimistic, we can look at the list of EDH cards in Modern Masters 2015, pick the cards unlikely to get another reprint, and predict a rough 50 percent cut in price and a 50 percent increase from that floor price. Not great, but predictable.

What do we like for this effect? Out of the EDH cards in the set, few are truly safe from reprint, and few compare with Creakwood in terms of desirability. The Eldrazi have been reprinted before in various manners and don’t feel as safe to me, and their high buy-ins reduce upside. Kiki-Jiki may get reprinted every two years in this wacky set. Comet Storm in the only mythic rare anyone is opening if the hashtag #CometCurse is to be believed. Wilt-Leaf Liege‘s price is mostly predicated on a modicum of Modern play—Brian Kibler saying the name of a Magic card on Twitter has roughly as profound an effect on price as does all of EDH-dom, so I expect Modern to greedily swallow a ton of the loose copies irrespective of how much it’s actually played. If you disagree, Wilt-Leaf may be a good buy, but my money is on Creakwood. A lot of the rest of the cards on my list are pretty cheap.

Based on the response I get this week, I may clarify a few points on this topic before I move on to something else, so make sure you hit up the comments section. I am in Las Vegas until next week for the GP (in the loosest sense of being in Vegas “for the GP”), so I may not spend a ton of time monitoring the comments, but I will try and check in. Your feedback so far has been invaluable and I hope you continue to engage with this series and encourage others to ask questions. Come find me if you’re in Vegas and say hello! Until next time.

City of Traders, ProTrader, Unlocked ProTrader

UNLOCKED PROTRADER: Going Hunting on the Banned and Restricted List

1 Comment

By: Travis Allen

When this article goes live, I’ll either be in or en route to Las Vegas, along with what feels like what must be a quarter of the Magic-playing population. I haven’t been aboard the #hypetrain that three-fourths of my Twitter feed has been, mostly because I’m incapable of experiencing these “emotions” I hear people constantly have, but I’m looking forward to it nonetheless.

I suspect that my plan for the event is similar to many: I’ll participate in the main event because I’m there and it should be fun, but it’s hardly the flagship activity of my attendance. Other activities, all just as important, will be two-headed giant events with friends, social mixers with various Magic personalities I’ve yet to meet in person, distributing MTGPrice loot to a handful of individuals, writing up coverage about what’s hot on the floor, taking in a show or two, and maybe even hanging out at the pool in the naked desert sun. If you see me wandering around the floor, feel free to stop me and say hello. I’m always happy to meet the few poor souls that read my articles.

I’ve spent the last three weeks writing about Modern Masters 2015, so I’ll spare you from that this week. After all, big price movements will be happening after all the events wrap up and tens of thousands of cards end up hitting dealer buylists or local binders across the world. A week or two after the festivities will be a good time to check in on MM2015 again. In the meantime, let prices settle a bit, enjoy the draft format, and see what else is going on.

No Reservations

With Dragons of Tarkir fully in the rear view mirror and Origins a good six weeks away, we’re smack dab in the middle of Standard set releases. This makes it a good time to discuss cards whose value can and frequently does run up close to release dates. I’m speaking of cards on the banned and restricted (B&R) list.

It seems that nearly every regular set release is accompanied by B&R speculation. What’s coming off the list? Are they finally banning card X? Was last weekend’s GP enough to push them in one direction? What would be good if format Y gets card Z back? And so on and so on. Speculation runs rampant. People make absolutely ridiculous claims about what would be fair to unban and how good the card would or wouldn’t be if legal.

Perhaps a bit anecdotal, but it feels like Modern chatter is cyclical to me. A set release will bring with it extensive B&R speculation, and when the article finally goes live on DailyMTG, we get an answer one way or another. Banned cards hit buylists within minutes, unbanned cards are bought out even faster, and social media fills with complaints about dealers that cancel orders. Unbanned cards mostly fail to make an impact and prices slowly fall away over several months. Golgari Grave-Troll is a perfect recent example of this.

ggt

By the time the next set release rolls around, nobody seems to be talking about anything. I often forget that it’s going to happen until a day or two beforehand. The article is posted, no changes are made, and life goes on, at least until the next update is two weeks away and the speculation mill starts up again.

Back when Fate Reforged was on the horizon, everyone thought Bloodbraid Elf was coming back. Check out the price graph:

bbe

What’s amusing here is that 90-degree turn in the red circle is about a week before the update occurred. Rather than waiting for the update to find out if BBE would actually come back, people began moving in hard entirely on speculation. The update came and went, BBE stayed banned, and now we’re back to about $4, half the price of its frenzied peak, and double-ish the pre-rise lows.

Movement on cards ahead of B&R updates is happening earlier and earlier, and is exactly why we’re talking about this in the middle of two set releases, when speculation on the list is at its lowest. The time to buy cards coming off of the B&R list isn’t seconds after the update—everyone and their dog is trying to do that. Somewhere between a fraction to all of your orders will get cancelled, and you won’t have the cards until after the prices have already started to settle. If you really want to profit on B&R list updates, waiting until the list changes is a fool’s game. Action is required when nobody else is paying attention—now, essentially.

This is the primary lesson of today’s article. You don’t make money by buying cards immediately after updates. You make money by picking up cheap copies when nobody is looking, and then selling everything you have the second it’s unbanned.

brilliantplan

Private Reserve

The secondary component of this article is looking at what’s on the B&R list today that’s worth picking up. Two key factors on this exercise: there’s no certainty whatosever in this process, not in the way that “Tasigur is going to go up” or “reserve list cards are safe” are certain. A card could be considered by the entire community to be impotent in a format and undeserving of a ban, but until WOTC scratches the name off the list, it’s going to languish in the bulk bin.

The other factor is urgency: there is none. You don’t have to run over to SCG or TCG or ABU or whatever immediately after reading this and go deep on Black Vise. My preferred acquisition on B&R targets is slower and less deliberate. If I see one in a trade binder, I’ll pull it out. People are often happy to move a card that has no immediate applicability. If I’m placing an order for something, I’ll see if they have any of my preferred banned cards in stock at reasonable prices. I also scan big sales like SCG’s back-to-school  for discounted cards on the list. Hall off on Mind Twist? Sure, why not.

All of that said, what’s currently on my watch list?

Modern

Bloodbraid Elf
While she missed last time, I’m confident that we’ll see her again eventually. There’s a good reason her price ran up so high before: a lot of people think she’s completely fair to add back into Modern, especially with the introduction of Siege Rhino as competition at the four-slot. If a portion of the community thinks that she’s fair to reintroduce to civilized society, there’s a good chance a few decision makers over at WOTC feel the same way. Also consider that when BBE was banned, Deathrite Shaman was legal. now that DRS is gone, the Jund strategy that BBE was supposedly propping up has mostly disappeared, replaced instead by Abzan.

Before the huge run-up in price, I liked FNM copies at $3 to $4. Post-surge, this price has stuck a lot closer to $10, unfortunately. While promos would probably hit $20 or more if she was actually unbanned, I like the normal copies more right now. They’re considerably cheaper, with $2 copies available if you look, and these will spike to $10 or more should she return. It’s also a lot easier to pick up a few $2 copies here and there than $10 copies.

Green Sun’s Zenith
With Birthing Pod’s departure, there’s a lot more room in the format for GSZ. The largest roadblock to Zenith returning is Dryad Arbor, as a single Arbor in your deck means that GSZ is always a better Llanowar Elf on turn one. A popular solution is to ban Dryad Arbor, which adds absolutely nothing to the format right now, and unban GSZ (hell, it’s worth banning just for that FTV: Realms art. How a card that deceptive passed inspection is beyond me).

Admittedly, this card was more interesting last year, while the price was still south of $5. Since 2014, we’ve seen the buylist increase significantly to keep pace with what appears to be casual and EDH demand. That’s good news, though. A solid demand profile without existing competitive appeal means that we’re unlikely to get burned holding copies, and prices could continue to rise from other sources while we wait for an unban. If this ever comes back, I expect prices in the $25 to $35 range out of the gate, and I’ll be right there with every copy I have.

Jace, the Mind Sculptor
I just want to take a moment to say that this is actually a terrible card to pick up on unban speculation. WOTC’s offices would be burned down if they unbanned Jace without printing a butt-ton more copies at the same time. Stay away on Modern speculation.

Legacy

Black Vise
The fact that people are scratching their head on this card every three months bodes well for Black Vise. Listening to people that know more about these strategies than I, it seems that this card is a completely fair addition to Legacy. A facet of the card is that it provides a way for burn strategies to beat up on combo decks that don’t manage to go off immediately, which is helpful in a matchup that currently leans heavily in combo’s favor.

With both Fourth Edition and Revised printings, there’s no shortage of copies out there. I’m targetting FTV copies, since it’s the only foil that exists. At $2 each, this is an easy $5 to $15 card should it get unbanned.

Mind Twist
Losing your entire hand to someone on turn one or two is the biggest fear with regards to Mind Twist. Some combination of land, Dark Ritual, Grim Monolith, and maybe another rock or two means you can take five to seven cards out of an opponent’s hand before they can meaningfully interact. However, under a slight bit of scrutiny this fear is easily allayed. A single Force of Will completely screws the guy casting Mind Twist, since he went all in to cast it, and his opponent is now only down two cards instead of six. And even if the Twist resolves, what’s left to do? The Twister casting it has a land, and maybe a mana rock or two left over, while the Twistee has maybe one card remaining. Advantage goes to the Twister, sure, but it’s not like the game is locked up. Both players are in top deck mode. Land, land, Tarmogoyf out of your twisted opponent is going to suck big time.

At $2 to $3, the buy-in is quite low. Like Black Vise, we’ve seen this in Fourth Edition and Revised, but at rare rather than uncommon. Concerns over the card being too good will abound in the days following the unban, with plenty of dark mages looking to play Twister in the near future. This will be $10 easily with a return to Legacy.

Mind’s Desire
I really doubt it, but I’ve got a small stack just in case. With only a judge promo and the original Scourge copies on the market, and a nearly guaranteed four-of status in any deck where it sees play, the reward is high enough for the risk that this never comes back.

Got Any More?

These are my current favorite B&R list targets these days. I’m curious to hear arguments for other options in the comments. Remember that the best time to scoop up these types of cards is exactly when nobody is talking about them. Set alerts on your calendar to remind you when to start looking if you have to.

As for those of you heading off to Vegas: see you on the floor!

ProTrader, Sigmund Ausfresser, Unlocked ProTrader

UNLOCKED PROTRADER: Make Money By Going Nostalgic

14 Comments

I remember 1993 as if it was yesterday. The World Series was won by a Canadian team, the Toronto Blue Jays. Canada also took down a Stanley Cup, something they haven’t done in a while, via the Montreal Canadiens. It was the year of “Got Milk?” and Mrs. Doubtfire was outclassed only by Jurassic Park in the movie world.

According to http://www.pop-culture.us/Annual/1993.html, “The Habit” of 1993 was a little collectible card game called Magic: the Gathering.

 

Shivan

Anyone who played Magic in the early-to-mid 90’s remembers wishing this card was in every pack they opened…ok this isn’t precisely the case, but I sure remember wishing I owned a copy of this top-end creature. Even now, 20 years later, I feel incredibly nostalgic when looking at my favorite classic cards. That nostalgia is my primary motivation for maintaining a separate “not-for-trade” binder. The binder isn’t about value, though there are certainly some valuable cards inside. It’s more about cards I’ve enjoyed as a kid or cards with artwork I love so much that I want to keep a copy of the card forever.

In the “New Age” of Magic — Modern Masters 2015 reprints, flashy sets filled with Dragons and computer-generated artwork — my nostalgia for classic cards and art grows continuously.

And it seems I’m not the only one who feels this way…

Welcome to Old School (93/94)

From http://oldschoolmtg.com/, here’s a brief overview of the format:

“93/94, Old School Mtg, started 2007 in the casual Magic scene in Gothenburg, Sweden, and have since grown with players across Europe and North America. A total of seven sets are allowed in the format: Alpha, Beta, Unlimited, Arabian Nights, Antiquities, Legends, and The Dark…” [SIC]

Essentially, this is a fledgling format all about enjoying the Magic of yester-year. While technically I didn’t start playing Magic until 1997, I can still appreciate the concept of a format based around the earlier days of the game, where cards like this were highly relevant:

Icy

“Seriously? During the release of the most financially impactful set of all time, you’re going to write about Alpha Shivan Dragons and Beta Icy Manipulators?”

Yes, for two reasons.

First, I am 100% confident you will be inundated with Modern Masters 2015 articles throughout the week. From strategy and how to build a sealed pool to what cards to sell immediately to what cards to acquire, it’ll all be covered by my esteemed colleagues here. While I could be content to share my thoughts, I suspect they’ll overlap tremendously with the rest. Frankly, I’d prefer to write something unique that will bring new perspective to MTG finance.

Second, I suspect there is some very relevant financial information associated with this nostalgic phenomenon. More and more players are talking about older cards and I’m noticing my Twitter feed is filled with this buzz. But there’s no explosion of interest yet – I would go out on a limb and suggest this isn’t even as big as Tiny Leaders, which is arguably more hype than actual format. That being said, getting into this format on the ground floor is absolutely critical.

Don’t care about a nostalgic format? Too young to remember casting Juzam Djinn and Hypnotic Specter? This may not be important. I’m not here to sell you on a (yet another) format; I’m writing this column to drive awareness of a small trend with potential for profound financial impact. This is about getting in front of the curve.

Some Observations

Doctor Superstition (@DSuperstition) is an active member of the Old School Mtg community, and he’s been tweeting some curious observations of late.

Tweets

These comparisons fascinate me. They may not be incredibly successful in converting players to Old School MTG, but they present some intriguing, hypothetical trades — even highly relevant trades, considering all the MM2015 booster packs that are about to be opened. Imagine opening a Mox Opal at GP Vegas, only to be offered a Beta Hypnotic Specter in trade for your sweet pull. Would you do it?

Mox Opal

Hypnotic

As Doctor Superstition pointed out, the two cards have roughly the same value. But looking at the charts above, which one would you rather sit on for the long term?

Ok, so it doesn’t take much to convince folks that old-school cards are safe to hold for the long haul. Everyone can look at charts like those above, comparing MM2015 reprints and playable Beta cards, and make this same conclusion. That’s not the most breakthrough observation, I’ll admit. But it does plant a seed in the back of my mind for when I’m in Vegas…

The “ah-ha” observation comes from looking at other charts for Old School Mtg cards alongside the current stock of major retailers such as Star City Games.

Consider Tawnos’s Coffin, for example, which is seemingly sold out across most the internet.

Coffin

This is the buyout that no one is talking about. The Antiquities artifact is sold out mostly everywhere, and you can see how both the value and buy list price jumped simultaneously, a sign of very positive upward momentum. This isn’t some forced buy-out here – this is a move backed by retailers. And you can bet the farm that when SCG restocks this card, it’ll have a much higher price tag than its current $24.99 one.

Of course, the trend on Tawnos’s Coffin could be a fluke. It’s a powerful Commander card, so maybe people are finally discovering it? It’s plausible, but I don’t believe Tawnos’s Coffin is the only old-school card suddenly gaining interest.

Old Man

This is one I’ve been highlighting on Twitter lately. Old Man of the Sea’s price seems stagnant when looking at the green curve. But when you assess the blue curve, indicating top buy list price, you can see a noteworthy incline. Retailers are having a tougher time keeping this creature in stock, and it won’t take much to see a sudden spike here as we did with Tawnos’s Coffin. Though it’s worth noting Star City Games has nine total copies in stock with NM listed at $59.99 (this is $10 higher than the price was a month ago).

One of the neatest Old School Mtg card is Chaos Orb, which has also seen significant buy list increases over the past couple years, including one earlier this year.

Chaos Orb

I hear it’s not easy to keep nice copies of this rare artifact in stock. Star City Games is completely sold out of the most affordable Unlimited version, with a NM price of $99.99.  This card seriously deserves more attention than it is currently getting.

The three examples above highlight an important trend – these nostalgically popular cards are destined to increase in price. This should come as no surprise to people. What’s critical to consider, however, is the potential impact an Old School MTG format could have on some of these prices. Let’s face it – there aren’t many Chaos Orbs and Tawnos’s Coffins out there. Any spike in demand, no matter how small, could have a profound impact on card prices.

I’m not here to incite a buyout. If people were to suddenly start speculating on these cards like they did on Tiny Leaders, it could prove detrimental to the health of Old School MTG. Availability is a major consideration here.

But I am trying to inspire you to consider adding a few of these cards into your MTG portfolio. They provide tremendous stability with significant upside. In fact, I’d probably rather have a few Chaos Orbs than, say, a couple booster boxes of Modern Masters 2015. I believe there is much greater upside and lower risk to the former. MM2015 boxes may be good investments eventually, but with so many unknowns right now in this unprecedented time, I can’t help but encourage caution.

Wrapping It Up

Thus summarizes my strategy heading to GP Vegas. Some players will be anxiously dumping the pulls from their MM2015 booster packs. Others will be keenly aware of dropping prices, attempting to pick up their Tarmogoyfs and Vendilion Cliques at a favorable price. While I have a short Modern shopping list myself, I’ll be most interested in picking up some of these older cards.

The reason for this move has nothing to do with my desire to play Old School MTG (although it does sound like a fun format). Rather, I’m noticing a gradual trend towards these nostalgic cards and I recognize that any spurt in demand could lead to drastic price fluctuations. A small surge in Tawnos’s Coffin interest has caused one retailer to double their buy price overnight. ABU Games and Star City Games are two vendors that do not like being out of stock of these older cards – if that trend occurs too frequently, they WILL up their buy prices.

By keeping an eye out for deals now, and trading strategically into some of these nostalgic cards over time, you set yourself up for strong portfolio growth going forward. And if this 93/94 format ever does grow legs, you could be looking at some surprising double-ups. Even if that doesn’t happen, collecting stuff like Guardian Beast and Island of Wak-Wak is just plain fun. With most of these cards also being on the Reserved List, you can be confident your investments will, at a minimum, hold their value.  Cards like these remind me of what initially got me into Magic. Collecting these cards and then making bank on them would just be icing on the cake.

…

Sig’s Quick Hits

Here are a few other Old School Mtg cards I have my eye on for GP Vegas:

  • I mentioned Guardian Beast towards the end of this column. The Arabian Nights creature has increased in value by about $10 over the past year. But what really interests me is the top buy list price, which has been steadily increasing throughout 2015. SCG has three total copies in stock, with zero being NM ($79.99 price tag). If you want a copy, why not trade into one soon?
  • Dark Ritual has been printed a billion times. You can find hundreds of copies for $0.50 throughout the internet. But how many Alpha copies of the black instant can you find? None at Star City Games, where they are sold out with a $39.99 price tag. Yet again I see the top buy list price steadily rising over the past 6-12 months despite choppy action in estimated value. I have to imagine this card is a power-house in Old School MTG, and definitely worth keeping an eye on.
  • Speaking of cards that have been reprinted a ton, City of Brass is also worth closer inspection. The original printing of this Nonbasic land has been on a steady incline over the past couple years as well. Did you know this card retails for $79.99 now?! Star City Games has a handful of copies in stock, but finding NM copies can be quite difficult!
  • BONUS TIP: Want to go real deep? Reviewing some of the top decks of the 93/94 format, it looks like Su-chi is a popular card. The artifact creature is an uncommon from Antiquities, so it’s not as difficult to find as some of the other cards I’ve mentioned earlier. But the top buy list price has jumped from $2 to $3 earlier this year. SCG has 17 total copies in stock, with only 1 being NM at $5.99. It probably wouldn’t take much to manipulate this card’s price, but I’d much rather be in the camp of obtaining my set now and sitting on them for a couple years.
Accumulated Knowledge, ProTrader, Unlocked ProTrader

UNLOCKED PROTRADER: Modern History 101 – Eighth Edition and Mirrodin

3 Comments

BRIEF TEMPORAL ASIDE: I’m jealous of all of you who are reading this, because you are living in a time when Modern Masters 2015 has come out, while I am currently trapped in the past. Are you gonna crack some packs? I know I am! Cracking packs is so much fun.

Rather than talking about Modern Masters 2015, I want to talk about Modern itself. A lot of writers have done individual set or block reviews (myself included!), but I don’t think there has been a narrative overview of what Magic was like when those sets were out. We are going to do that, and compile some information that often gets discarded. You’ll see what I mean as we go along.

 

Eighth Edition

This was the first set to feature the new card face that would later go on to kill Magic1. The set, like all pre-M10 core sets, was comprised entirely of reprints. The selling point, though, was that this set would contain one reprint from every previous Magic set that had not been in a core set already. Neat!

And while several of those reprints are underwhelming on the order of Vexing Arcanix and Skull of Orm, there are some good cards in this set! Blood Moon was first reprinted here (and later again in Ninth), and Eighth Edition put such gems into Modern as City of Brass, Intruder Alarm, and Ploooooooow Uuuuuuuuuuuundeeeeeeeeeeeeeeer (I really like casting Plow Under).

Other finance gems worth noting include Planar Portal, the Urza-tron lands, and foil copies of Fecundity, Merchant Scroll, and Vernal Bloom. The first Standard format that Eighth Edition came into was Odyssey/Onslaught/Eighth, and neither of those expert-level blocks are Modern legal—if you want to see what the format looked like, check out the 2003 World Champs. Oh, and they made a big deal about the prerelease (even though the promo was Rukh Egg), and I won mine.

Non-Foil Cards of Note

Blood Moon – This card is in good Modern decks and bad Legacy decks.

Ensnaring Bridge – Modern, Legacy, Cube, Commander, Casual.

Bribery – Commander only. [Editor’s note: Cube would like to have a word with you, Ross.]

Grave Pact – Commander only also.

Lord of the Undead – I’m beginning to sense a pattern.

Defense Grid – Mostly Commander, some Modern.

Elvish Piper – Commander, and the eventual inverse of Tiny Leaders (Okks?).

Coat of Arms – Commander and any weird tribal format.

Choke – Modern, Legacy, and anything that is dominated by blue.

Foils of Note that Aren’t Just the Same as Above

Birds of Paradise – I’m not entirely sure why, but this is one of the most expensive printings of Birds. Seventh Edition foils blows these out of the water, though.

Storm Crow – I hate that the Storm Crow people have made this happen. Retail “price” of $32, best buylist price of $4. One of those prices is off, and I think it’s the first one.

Merchant Scroll – Vintage!

Teferi’s Puzzle Box: Casual favorite, I suppose?

Ambition’s Cost: Only foil printing of this card.

Noteworthy Standard Decks

NONE.

Now, I do love me some UG Madness2 and some Goblin Bidding, but that’s not really what this section is going to be for. As we roll into future sets, I’ll mention any decks that I think may be worth having on a resurrection radar—maybe an old archetype could benefit from new technology! I don’t expect much, but it’s worth looking. Also, I’ll be able to tell you if a deck was the real deal (like Karstenbot) or bogus (like Ghost Dad).

Analysis

There are a lot of foils in this set that are worth money, and there are fifteen rares worth $3 or more. The downside is that the set had 111 rares, so only about ten percent of the rares are worth the typical price of admission. There are some major wins if you hit on a foil, but I’m not going to tell you to buy a bunch of old packs to hopefully open a foil rare.

This set, despite its gimmick, was not super popular, since most of the marquee cards at the time (Persecute, Birds of Paradise, Wrath of God) were cards that enfranchised players already owned. Sealed packs look to be between $5 and $8 (ignoring shipping), so that’s not quite low enough to look appealing. If you are a gambler, and your local store has had these on a shelf since 2003, maybe they’ll take $3 each just to clear up space, but even then, 111 rares is a lot. To compare, there are 73 rares and mythics combined in M15, and only 68 rares and mythics combined in Dragons of Tarkir. If you open a box and each rare is different, you are only going to open 32 percent of the rares in the set, and only about three to five of them are expected to be “hits” (versus the lower price of entry, if you can even get it).

The prudent thing to do is to stay away, which means that these cards are going to slowly keep creeping up in value. All of the cards in here are prime candidates for reprinting in a future Modern Masters or Commander product (it’s already happened for some), although some of the more powerful cards, like Plow Under, are unlikely to ever be put in Standard again.

Oh, and I’ll mention this now since we were talking about packs: don’t forget that the foil distribution process didn’t change until Planar Chaos (where the foil replaces a common), so if you open a foil rare, that is also your rare. You can’t get two rares.

Parting Words

Don’t buy packs, do look up any foils that you see in longboxes where you don’t already know the price.

Mirrodin

This was the first expert-level set to feature the new card frame, and, to be fair, did a pretty good job as a block trying to kill Magic. This was also the first set to leave Dominaria in a long time, and we wouldn’t return until Time Spiral. The block’s theme was “artifacts matter,” and the books were terrible. I don’t want to talk too much about the block as a whole, since we are going through sets individually, which will probably help me limit my hateful vitriol to Darksteel where it belongs.

Mirrodin introduced affinity, equipment, and Mindslaver to Magic, so it certainly has had an impact. The set definitely had hype going into release, and the massive amount of design space devoted to cool artifacts has definitely given the world several casual favorites. The prerelease card, Sword of Kaldra, was a big hit with the Timmy/Tammy crowd, and the only reason it isn’t worth more is because I doubt most newer players are aware it exists3.

I remember Mirrodin pretty well, because it was around the time I started FNMing weekly as a priority. Like Eighth Edition, much of the analysis of this set in terms of Standard is going to be warped by the inclusion of sets that aren’t Modern legal (in this case, just Onslaught, one of the coolest blocks ever), and also by the fact that several of the best cards in this block got banned. I remember FNMs were getting pretty big around this time (I hopped between a few different stores). If only they knew what was about to happen…

Non-Foil Cards of Note

Chalice of the Void – Took off as anti-Treasure Cruise technology, and hasn’t come down since. The card is very good in older and more cutthroat formats like Legacy and Vintage, since there are more aggressive forms of “fast mana.” This card was a player in Old Extended with the next card on the list.

Chrome Mox – It should not come as a surprise that when WOTC uses the word “Mox” in a name that the card is very good. This card is considered to be too good for Modern, but it’s about right in Legacy, since going down an extra card when you play it is more taxing. Something to notice on Chrome Mox and some of the other top cards on this list: the buylist prices are all very good. Often a smaller spread between a buylist price and a retail price can mean copies are viewed as easy guaranteed sales, which you can extrapolate as expressed confidence in the card in the long term. If the big dealers like something, then you probably should too.

Oblivion Stone – This card went from zero to hero with the advent of EDH, and has cemented a place in Modern with the consistent success of Tron decks. Two big populations like this card, and it’s pretty good in Cube, too. This is basically Nevinyrral’s Disk to a generation of players. That’s a good thing.

Glimmervoid – Some versions of Affinity play lots of spells of different colors, so this is pretty much their best land.

Tooth and Nail – If you resolve this in Constructed, you win. There are lots of different two card combos to find with Tooth and Nail, but I’ll always have a soft spot for Mephidross Vampire and Triskelion. For a while, Tooth and Nail was an easy twenty bucks, so don’t be surprised if the current price of $8 balloons up again.

Duplicant – Popular EDH card and actual spot removal spell in Vintage (you can cast it off Mishra’s Workshop!). Yes, this is why the foil price is insane.

Platinum Angel – Despite a couple reprints, this is one of those marquee cards that is always going to keep a respectable price. “You can’t lose” is pretty appealing to most Magic players and/or Parker Lewis.

Sculpting Steel – Another card that is good because of Mishra’s Workshop, although this has largely been co-opted by Phyrexian Metamorph.

Goblin Charbelcher – Best card in Magic.

Foils of Note that Aren’t Just the Same as Above

Solemn Simulacrum – This is the original set foil version of this card. Sad Robot, perhaps, but at that price, I’d be smiling.

Lightning Greaves – EDH staple, or at least it used to be. Also original set foil.

Mindslaver – The other best card in Magic.

Thoughtcast – Again, original set foil. This card is crucial in Affinity decks, since playing your entire hand at once typically becomes a disadvantage if the game goes on for much longer.

Sylvan Scrying – Original set foil, finds Urza lands and other toolbox effects. Played as a 4x in a few Modern decks.

Talisman of Dominance – Played in Legacy, believe it or not.

Molten Rain – This card hasn’t been in either Modern Masters set yet, which is surprising. This card is very good, and I’m surprised the foils are only $10.

Noteworthy Standard Decks

Broodstar Affinity – It didn’t take long (by 2003 standards) for Affinity to be uncovered as an extremely unfair mechanic. The five artifact lands, in concert with Disciple of the Vault and Atog (yes, really), helped enable some extremely degenerate strategies.

The decks also featured Broodstar, a heavy-hitting beater that would get in large chunks of damage coming down extremely early. Broodstar was a serious threat, and is probably the only Affinity-era star to not get serious consideration in Modern. The reason why is likely because Affinity decks now lean towards strategies that better support Cranial Plating, which encourages a wide threat of small artifact creatures, rather than just a bunch of artifacts. I’m not sure if Broodstar adds anything to existing Affinity strategies or if building a new version around the flier is worth exploring, but Broodstars are currently dirt cheap and Affinity is very popular in Modern (and Legacy!). Much of the other stuff that was in these lists was later replaced by better cards in the other two sets (sorry, Scale of Chiss-Goria).

RDW – Red decks are always going to try to be as lean and redundant as possible, so it’s hard to find something that is “hidden” in terms of red deck technology. Molten Rain is probably as good an example of a hidden gem as red decks can get, which should tell you how little meat is still left on the bone. Arc Slogger does not belong anywhere near your Modern red deck. Slith Firewalker is probably not even good enough, which stinks.

Analysis

Looking through the foil prices on Mirrodin, I started to realize how many good cards there are in this set. While you can never truly judge a book or a Magic set by its cover, I think it actually makes thematic sense that Mirrodin has a wide variety of cards with casual appeal. Artifacts, by their nature, are accessible to decks of every color, so the demand is more widespread—if something is good, it’s a card that all EDH players want, not just ones playing blue (like Bribery) or green (like that dumb creature that does a thing). Put a pin in this topic, we’ll come back to it in a bit.

Anyway, boxes look to be about $250, which puts packs just shy of $7. There are only eleven cards that beat that mark (or come super close, like Sculpting Steel), so buying packs is a losing proposition once again (this is often going to be the case). There are a few uncommons and commons of value in the set, including Wrench Mind, which is the closest Modern is ever going to get to Hymn to Tourach4. This is a great set to pick through when you are looking at bulk, and there are a handful of cards out of this set that may be worth a closer look (I’ll be changing the way I do my set reviews to better fit this new series in the future, so they are complimentary pieces rather than basically writing the same thing twice).

It’s worth mentioning once again that Mirrodin on release was a very popular set. Standard was still heavily defined by Onslaught, but that set, while it featured some pretty powerful strategies, wasn’t so strong that it overshadowed new tech. There were a lot of people, myself included, who were just happy that Odyssey block was gone, if you can believe that. Those sets were cool, but rewarded thinking in a way that was only clear to very good players.

Coming up next: the set that would send the tournament player base into a nose dive.

Two Sets Down…

Let me know what you thought of today’s article. It’s fun to go back and parse out what we didn’t know when all this was happening, and I try to interject what I remember personally (this will get easier as we progress and sets are more recent in my memory, except for those years where my LGS was next to an Outback Steakhouse that did happy hour right before FNM). If there is something you’d like to see me add, or you’d rather me just stick to our old set reviews, let me know. Thanks, and I’ll see you next week!

Best,

Ross

P.S. Word is that it is possible to reseal Modern Masters 2015 packs. Do not buy packs from someone you don’t trust completely, and be extremely scrupulous. Also, as a way to be respectful to other players, don’t discard the packaging in a way that other people may be able to reuse your packaging. And make sure to actually recycle them! That’s what this change was for in the first place.

P.P.S. Sounds like cards are coming out of the packs with scuffing and damage. This is likely due to the new packaging method. More on that as it unfolds.

P.P.P.S. Remember when I said to put a pin in what we were talking about before? Here’s the elevator pitch version of every Modern block in three words. Tell me which jump out as the best sets for casual cards:

  • Mirrodin: Lots of artifacts!
  • Kamigawa: Lots of legends!
  • Ravnica 1: Ten color pairs!
  • Time Spiral: Sure, why not?!
  • Lorwyn: Lots of tribal!
  • Shadowmoor: Lorwyn minus tribal!
  • Alara: Now three colors!
  • Zendikar: Lands and Cthulhu!
  • Scars: Mirrodin plus poison!
  • Innistrad: This is Halloween!
  • Return to Ravnica: You loved Ravnica!
  • Theros: Remember Homer’s “Odyssey”?
  • Tarkir: Wedges and dragons!

1 Clearly it didn’t, but that was the assumption.

2 This was also the name of one of Magic’s few webcomics. I really liked it, and it’s where I got my Mise shirt.

3 The concept of exposure is something we’ve been talking about on the forums lately.

4 Although I’m holding out for an eventual “dinosaur world” set featuring a functional reprint named “Hymn to Turok.”