By: Travis Allen
Journey Into Nyx is upon us with prerelease events just a few days away. Does anyone else feel like we just did this for Born of the Gods? I’m still nowhere near knowing all the cards in the BTT draft format, and here we are adding a whole new pile.
A few words before we jump in. First, the dynamic of this block structure is familiar to veterans, but may actually be new to a good deal of rookie players. The big/small/small structure is the “normal” structure, but the last time we saw it was actually Scars of Mirrodin! We’ve added a whoooooole bunch of new players since then, so things are going to be a bit different.
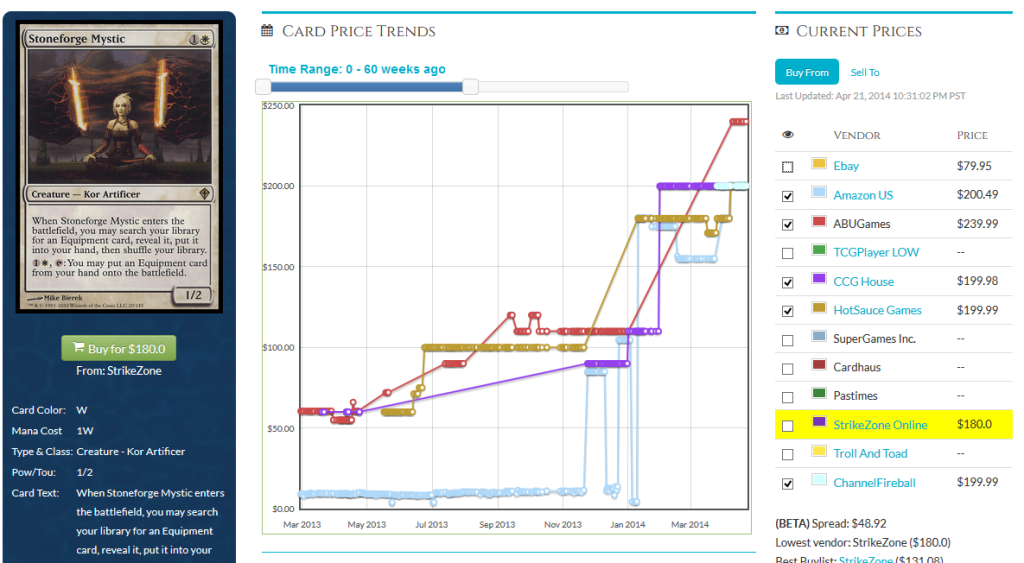
Cliff talked about it in the past, and I’ve mentioned it as well, but it bears repeating: the ratio of packs opened for Theros:BoG:Journey will be 6:2:1. That means that (roughly) for every six of a rare opened in Theros, only one will be opened in Journey. This will have a real impact on the price, although by how much remains to be seen. Keep this in mind as the prices unfold over time. What would have been a bulk rare in the past may actually hold a price tag of a few dollars. I tried to accommodate for this effect in my pricing, but I may have been too conservative. Watch the prices closely, and if things aren’t dropping by as much as you or I thought they would, then we know it’s having a dramatic impact.
Speaking of bulk, everything I put there I expect to be about a dollar or less. Some of it may end up doing a little better because of casual markets (Dictate or Erebos) or the metagame may shake out in a way that it’s actually reasonably represented (Setessian Tactics.) I’m not dismissing these cards out of hand, I just think that it’s likely most of them won’t end up doing enough to matter in the next six months.
I’ve only given prices out through six months because I’m not prescient. What the format looks like after the fall rotation will be so different that it’s impossible to know at this point which meta-dependent cards will thrive and which will fall by the wayside. We’ll reconvene after the block Pro Tour and see how things are looking at that point.
White
Bulk:
Dawnbringer Charioteers
Dictate of Heliod
Launch the Fleet
Skybind

Aegis of the Gods
1-2 Months: $1
Rotation: Bulk
Aegis of the Gods looks a lot more exciting than it is. True Believer has been in Legacy and Modern for quite some time and sees no action, so Aegis isn’t bringing much to those formats they don’t already have. Yes, Leyline of Sanctity is awesome, but that can be cast for free and doesn’t die to Bolt. That leaves only Standard to drive this guy’s price. If your opponent plays with Thoughtseize and has reason to fear this guy, they can still fire it off on turn one of either the play or the draw to make sure they nail your whatever.
Aside from not really solving the Thoughtseize problem, there’s still not going to be a lot of decks that would want this ability on a small body. He may show up here and there, and may even float around a dollar or two instead of bulk, but only from the barest casual support. Mostly narrow, single-format demand will keep his price low.

Deicide (Day-ah-side, not dee-side.)
1-2 Months: $1-$2
Rotation: Bulk – $1
A lot of people were very angry when this card was spoiled. “What of our gods?” they cried. Their lamentations filled Twitter. “Why punish us for worshipping?”
This is a safety valve, the same way that Grafdigger’s Cage and Glaring Spotlight and Renounce the Guilds were. Wizards has plainly proclaimed that they are keeping cards like this in formats at almost all times to ensure that nothing runs away with Standard entirely. Their goal is that the cards shouldn’t be consistently maindeckable, but if certain strategies get too strong they can be temporarily promoted to the front line. That’s exactly what we’ve got here.
Grafdigger’s Cage didn’t stop Birthing Pod from being played. Glaring Spotlight and Renounce the Guilds couldn’t stop Geist of Saint Traft. Deicide will occasionally punish people leaning hard on their god, but it isn’t going to mean the end of Thassa entirely. Athreos will still be entirely playable.
This is definitely reasonable enchantment removal, and may even see play as a one- or two-of in certain builds. It answers things like Courser of Kruphix or Herald of Torment nicely with an occasional added bonus. It doesn’t do squat against Desecration Demon or Polukranos though, so it’s not going to be saturating the format. It will see more play than Renounce the Guilds did, but not enough to matter. It will hang around a dollar or two for awhile as people grab their copies, but it will slip by rotation.

Godsend
1-2 Months: $4-$7
Rotation: $2-$3
Godsend looks pretty awesome but won’t play nearly as well as it reads. Any of the “Sword of Yin and Yang” are going to be better in Modern and Legacy, so that leaves us with Standard and EDH. +3/+3 isn’t the most threatening thing to tack onto a creature, so blocking is only going to be done in dire situations. Admittedly it makes a great rattlesnake on defense. But at six mana, does it matter? It’s expensive to play and equip, and offers no protection except against maybe Mizzium Mortars.
The preorder is high now because it’s splashy looking and sounds exciting. Lack of results will send the price crashing. It will likely hit “mythic bulk,” which is $1-$3. It may not be a bad idea to grab them at that point though. There are going to be very few copies in the market in general, and there should be enough casual demand after rotation (next year) to see it become a slow, sure gainer.
Blue
Bulk:
Daring Thief
Hypnotic Siren (unless it breaks out in Mono-Blue)
Polymorphous Rush
Scourge of Fleets

Battlefield Thaumaturge
1-2 Months: Bulk – $1
Rotation: ???
This guy is a real unknown for me. Will he break out, which is a very real possibility, or will he falter and fall flat on his face? He’s a got a reasonable cost and a reasonable body to go with it. 2/1’s are completely capable of doing work in constructed, as Snapcaster has proven. The real question is the unique ability that we haven’t really had much of in this fashion before.
Making your spells cheaper is always worth a very close look. The difference between 1B and B or 2U and 1U is pretty severe. Imagine Hero’s Downfall at BB and you’ll begin to appreciate what he’s capable of. How about this spell? “2U, Return three target creatures to their owner’s hands and Scry 1.” That’s limited all-star Sea God’s Revenge with Thaumaturge in play. Much more appealing at 2U rather than 5U, isn’t it? The secondary ability is probably mostly irrelevant. It will serve as a potential way to protect him from spot removal should the need arise, but right now there isn’t a lot in the format that would really make this silly. We’ll see what the fall brings.
I don’t think Thaumaturge will take off right away. There isn’t anywhere he belongs yet so it will take time for him to find a deck. Delver took some time before he had a proper home, after all. We may even have to wait for rotation and the subsequent cardpool/metagame to undergo a major shift. He’ll require the right enablers for sure. If we get the right mix of spells he’ll be a format role-player, but if we don’t get the tools he’ll be filling boxes of shame nationwide. His best chance today is probably going to be with Young Pyromancer.
At the end of the day, I’m pretty confident in predicting that he will matter at some point before fall of 2015. He’s got a reasonable body and a potentially absurd ability. With the quantity of JOU that’s going to be in circulation it won’t take much to push Thaumaturge into the $10+ range with only mild success, and $15-$20+ if he’s a rare Delver.

Dictate of Kruphix
1-2 Months: $1-$2
Rotation: Bulk-$1
Howling Mine effects have a history of being fairly popular. Font of Mythos is an $8 card. Dictate is a Mine with upside on the timing. You can hold up counters or removal or whathaveyou and only pull the trigger if you deem it appropriate. It’s certainly the best Mine effect we’ve seen since Temple Bell in M11.
However, Temple Bell is currently well under a $1 and was that cheap even before it was printed in Commander 2013. That’s pretty damning for Dictate. Temple Bell is very similar in that it’s the same CMC and your opponent doesn’t get the first card. On top of that, Bell also has the advantage of not requiring colored mana and is capable of being turned off if things get out of control. You need to ask yourself why the average player would ever pick Dictate over Temple Bell. I’m not coming up with much, how about you?
In Standard there isn’t too much in the way of flash decks floating around, so there’s not a whole lot looking for this effect. Control decks have things like Sphinx’s Revelation to play to, which are much safer when you’re trying to take control of a game.

Sage of Hours
1-2 Months: $3-$4
Rotation: $2-$3
First, the best part of this: in Standard, you can go infinite with Sage, the new Ajani, and Vorel. Ajani dumps three counters on Sage, Vorel doubles them to six, and then Sage gives you another turn. Rinse/lather/repeat. There’s typically a three-card infinite-mana combo floating around Standard, but there’s always the question of what to do with it. A three-card infinite-turn machine is another story. It’s clunky, but at least if you assemble it you actually win the game instead of passing turn with a billion mana in your pool. Of course with Thoughtseize in the format this is probably all irrelevant. Still, it’s at least worth being aware of if you spot some way to streamline the process and possibly make it competitive.
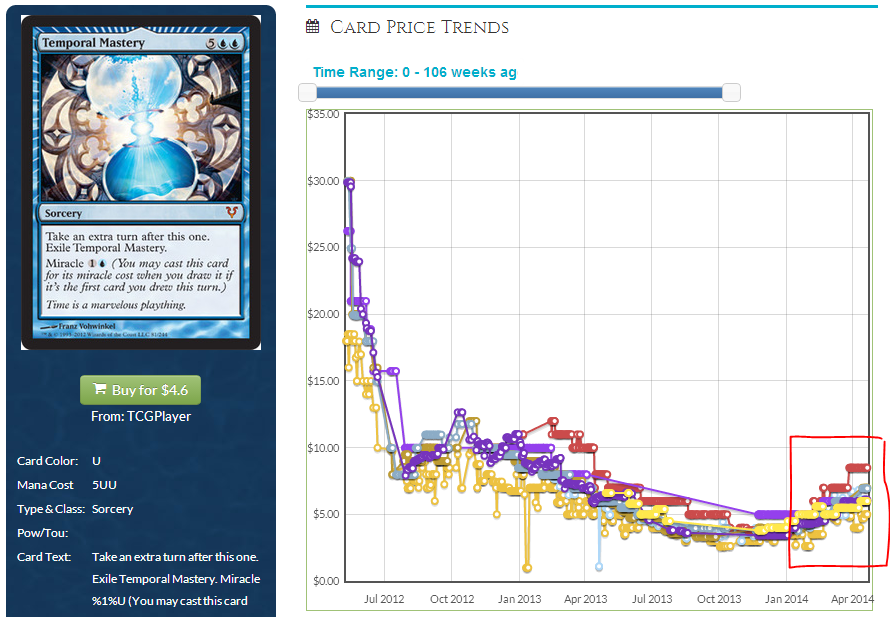
Outside of Magical Christmas Land, Sage should behave similar to most extra turn effects. He’ll preorder high, as the weeks after release roll by and the card doesn’t break the format it will sink towards a bit above mythic bulk, and then it will slowly gain from there on out. Make no mistake about it, without a reprint this card will be $10 or more by the end of 2016. If this guy gets down below $2, he’s a slam dunk so long as you’re willing to wait. Take a look at Temporal Mastery. See that tiny uptick at the end there? That’s not going to stop.
Black
Bulk:
Dictate of Erebos
Doomwake Giant
Extinguish All Hope
King Macar, the Gold-Cursed
Silence the Believers
Worst Fears

Master of the Feast
1-2 Months: Bulk – $2
Rotation: Bulk? $10?
Master of the Feast is a curious one. It’s easy to compare him to Herald of Torment and Desecration Demon. He’s inexpensive, a real threat in the air, and comes with a drawback tacked on. This formula isn’t new to us. The real question is how rough does the drawback have to be before it’s too much to deal with? Herald of Torment’s one life per turn is not preventing anyone from casting him, although he’s not quite as abstractly powerful as the other two. Desecration Demon’s seems pretty severe in text form, although it quickly becomes irrelevant when the guy with the demon also has fifteen pieces of removal. Master of Feast’s drawback seems to be the worst of them all.
When you’re the guy trying to kill people with a 5/5 flyer for three, you’re racing their ability to answer him. Giving your opponent more tools to deal with your threat isn’t something you’re pleased with. If they gained two life each upkeep or returned a creature from their graveyard to their hand or something that you could mostly ignore it would be fine. But an entire unrestricted card each turn is always going to have a chance to matter .
The flipside of this is that the way he’s worded it isn’t as punishing as it could be. They don’t draw the card until your upkeep, which means that if they kill him with sorcery speed removal then they either offed him before they drew the card or they took five in the air. The basic tradeoff is that without an instant speed answer, for each card they get you also get an attack phase. That can add up to a lot of cards, but it’s a lot of attack phases for a 5/5 flyer as well.
Master of the Feast is going to be an all or nothing card. Either the drawback is going to be too much and he’s going to end up at total bulk, or he’s going to pull a Desecration Demon and climb to $10+. Either way, I think he’s hitting $1 before he gets his chance to shine so you’ll have some time to make a decision either way.
Red
Bulk:
Bearer of the Heavens
Dictate of the Twin Gods
Harness by Force
Spawn of Thraxes
Twinflame

Eidolon of the Great Revel
1-2 Months: $2-$3
Rotation: Bulk – $1
Probably more important for Legacy and Modern than Standard, Eidolon is a Pyrostatic Pillar on legs. In Standard your opponent can get a two-drop down ahead of this on the play and stall until they can take the game over with cards with four CMC or more. On the draw it will be more painful, but an otherwise vanilla 2/2 will be awfully vulnerable. If you’re the guy casting the Eidolon, remember that your opponent isn’t just going to jam small spells into it over and over. If they cast a spell that shocks them, they’re doing it because they think it’s worth more than the two life it’s going to cost them. On average I’d say you’re likely to get an average of much less than two damage from their ability for each Eidolon cast in Standard.
The Legacy and Modern implications will be different. Both formats are packed with small spells so he’ll have much more relative strength. He’ll die more often for sure, but at least anything that’s killing him is probably going to shock it’s controller.
The biggest issue financially is that there’s going to be exactly one deck in each format that wants to cast him. This isn’t like Courser of Kruphix that can go in any deck that makes green mana. Eidolon only goes in the most aggressive of red lists, which means the overall demand for him will remain lowish. I see him slipping towards bulk prices, but I don’t think he’ll get too far below $1 or so. I don’t believe that he’s a Vexing Devil or Goblin Guide, but he’s still better than Firedrinker Satyr. If he has a very slow descent or even seems surprisingly resilient after the honeymoon period is over, that probably means the casual market likes him, which will make him safe as a long-term pickup regardless of his tournament success.

Prophetic Flamespeaker
1-2 Months: $4-$7
Rotation: $8+
I’ll get this out there: I’m a big fan of Prophetic Flamespeaker. Any mythic that isn’t huge, flavorful or splashy warrants attention because it means it may be mythic due to power level. Prophetic Flamespeaker falls into that latter category. He’s got non-square numbers (a sign of significant balancing in development) and a lot of potential power. The hook, of course, is making use of it.
It’s easy to look at Flamespeaker and think that turn three feels late, or that he doesn’t win a lot of battles without help, or that his ability can miss. I think that it’s just as easy to do this as it was to look at Desecration Demon and see all the ways he would fail his owner and do nothing. Cards don’t exist in a vacuum though, and the support you pack your deck with has a huge bearing on how well they do. Sure, Flamespeaker is relatively unexciting when staring down Courser of Kruphix. What about when you slap a Madcap Skills on him? Or have RG up representing Ghor-Clan Rampager? Or you played Imposing Sovereign on turn two and their turn three play can’t block? Or you just Lightning Strike their X-3 and get in? Or you manage to get him down on turn two?
In case you missed it, that ability does in fact trigger twice if he gets in unblocked. That’s two temporary cards drawn for the turn. Here’s a scenario for you: Untap on T4 with Flamespeaker. Use two mana to slap Madcap on him, get in for eight damage, and exile your top two cards. One of them is a land, which you play, holding the land in your hand for next turn. The other is a Lightning Strike, which you use to kill one of their creatures or even point it at their face since you won’t be able to cast it next turn anyways.
Prophetic Flamespeaker doesn’t hand you wins, but he has a lot of raw potential to work with. A little bit of work is going to pay you handsomely. The only thing that is really holding him back is the RR in the casting cost. At 2R, he’d be the breakaway mythic of the set. At 1RR, he’s good but a little narrow. Hopefully he will be good enough to get away from only being viable in Mono-Red. If the mana can support him he could easily show up in any type of R/X aggro deck. Being a mythic from a small spring set as this, it won’t take much to get his price up. I think he’s going to come down from his roughly $10 preorder price in the near future, but will climb above $10 again when people start realizing how much power he puts on the table.
Green
Bulk:
Dictate of Karametra
Hero’s Bane
Hydra Broodmaster
Pheres-Band Warchief
Setessan Tactics

Eidolon of Blossoms
1-2 Months: $2-$4
Rotation: $3-$7
My windows are a little large, but bear with me. What are we working with here? Well, first of all it’s the Buy-a-Box promo. I spoke about this in my Theros review, and the sum of it is that BaB promos are usually pushed for constructed. If a card is a BaB promo, we need to pay attention.
So how good is it? Elvish Visionary is 1G for a 1/1 that draws you a card when it comes into play. Solemn costs four and gives you a card on his way out, but he’s got a pretty sweet front side too. Both were fixtures during their time in Standard and see play in other constructed formats, so we’re in good company on “ETB:Draw a card.” Blossoms is obviously not as amazing as Solemn off the bat, but few creatures will be. In Blossom’s defense it’s at least guaranteed to draw you a card and has the potential to get out of hand.
A turn two Mana Bloom gives you a turn three Blossoms with a guaranteed enchanment in hand for next turn and Bloom is repeatable cycle for G each turn after. That alone is fairly tempting. Courser of Kruphix is another excellent green enchantment, and Boon Satyr isn’t bad either. You’re likely not playing Mono-Green, so there will be other options as well. Hey, you know what got reprinted in Journey? Oblivion Ring. (Sort of.) The double green in the casting cost is also probably a good thing since it powers up Nykthos quite well. I recall really wanting a four mana draw spell when I was playing Gr Devotion after PT Theros, and this is pretty close.
I expect Eidolon of Blossoms to very slowly dwindle towards $2-3 but it may be sticky due to people wanting to try it out and likely needing three to four copies. I don’t think it will really get a whole lot lower than that as some people will always be interested. Beyond that, if it does turn out to be solid it will behave like Courser of Kruphix and Sylvan Caryatid. I wouldn’t get rid of these at the Prerelease, and if it’s the type of card you see yourself playing, don’t feel bad about trading for a playset. The worst that happens is that you trade for them at $2-$3 and they end up at $1.
Gold
Bulk:
Revel of the Fallen God

Ajani, Mentor of Heroes
1-2 Months: $17-$20
Rotation: $9-$13
Domri Rade has been a four-of in a tier one Standard deck for basically the entire time he’s been legal. He also sees light Modern play. Currently he’s about $25, his peak was $30-$35, and his floor was about $10. He averaged maybe $20 for the last eighteen months.
Ajani is not as good as Domri.
I’m not going to ramble about the nuances of his Standard applications because as the banner Planeswalker of the set plenty of other people can do it better than I. Suffice to say that he’s not going to perform as well as Domri. He won’t perform as well as Elspeth either, who is about $20. There will be your typical honeymoon period while people grab their copies and he gets tried in bant Planeswalkers, but for the most part when he does manage to show up it will be as a one- or two-of. As Xenagos has shown us, even mild play isn’t enough to keep the price of a Planeswalker over $10.
The one thing Ajani has going for him will be his relative scarcity. That may push his price a bit higher than we would normally see for a fringe Planeswalker. If he does about as well as I expect, he should mostly be in the low teens and even under ten. If he sticks around $15, it will be because of the spring set bump.

Athreos, God of Passage
1-2 Months: $20-$25
Rotation: $14-$18+?
Hoo boy, now that is a God. He’s aggressively costed, revives a previously-successful Standard archetype, and will be popular in EDH. Those are all markers of a hefty price tag. The only reason I’m not expecting $40+ is because there is a little too much else going on in this set for him to turn into a Voice of Resurgence.
People think Athreos is good, and for good reason. Because of that his price will be slow to fall. If he sees very little Standard play, I don’t think he can get much below $10-$13. If he’s part of a major Standard deck, expect him to stick closer to $20, or perhaps even more depending on how pronounced the small set effect is.

Iroas, God of Victory
1-2 Months: $12-$15
Rotation: $6-$9
Iroas is pretty threatening, don’t get me wrong. He’s got a huge front end and he makes blocking miserable for your opponents. My concern is that he’s not terribly versatile. He’s got the Koth thing going on where there’s only ever really going to be one deck for him, and even there it’s unlikely you’ll want the full set. People will play him, and there will be some casual appeal, but it won’t be enough to keep him inflated with several other spicy mythics and rares in the set. The small set effect should keep him above Nylea and Heliod, but not by too much.

Keranos, God of Storms
1-2 Months: $8-$10
Rotation: $6-$9
On the one hand, Keranos has the best or second best text box of all the gods this time around. He is always doing something that matters, whether it’s putting cards into your hand or draining your opponent’s board/life total. On the other hand he’s a little expensive and it will take some time for his ability to really take a game over. I think he’s nearly as playable as Athreos is, but unlike Athreos will likely not be a four-of wherever he ends up. We also don’t have a home for him to slot into right away which makes it tougher for him to maintain his current $10-$15. The best advice I can give on Keranos is to expect nothing in the short term, but pay close attention to the block Pro Tour.

Kruphix, God of Horizons
1-2 Months: $5-$6
Rotation: $3-$5
Ugh.

Pharika, God of Affliction
1-2 Months: $5-$7
Rotation: $4-$6
Pharika is preselling on Channelfireball right now for a whopping $7 so there obviously there isn’t a whole lot of hype surrounding her at this point. Most people are relatively unimpressed, but I’ve heard from a few intelligent people that there’s some silver lining here. She’s cheap with a nice fat body. She’s in green, so we can see her come down on turn two, potentially allowing you to put four colored mana symbols into play on turn three and swing for five. She recycles your dead bodies into threats, which is great in attrition decks, a common theme for GB. Perhaps most importantly and mostly under the radar, those snakes she puts into play are enchantments. That means they trigger constellation, such as on Eidolon of Blossoms or Underworld Coinsmith or Doomwake Giant.
Will any of that be enough to keep her above bulk god prices? Honestly, probably not. She’s going to slip before she rises again, and if she ever does make it back above $10 I don’t think it will be overnight. You’ll have time to react if she sees an uptick in play and price.
Artifacts

Hall of Triumph
1-2 Months: $1-$2
Rotation: $1-$3
Honor of the Pure, Glorious Anthem, and the colorshifted Gaea’s Anthem are all $1-2. This is considerably easier to cast at the cost of being a tad more narrow and legendary. Being legendary hurts, but being an anthem effect in colors that don’t normally get one is important. Mono-Blue could possibly be in the market for two of these, and decks running Prophetic Flamespeaker could conceivably be interested as well. I believe this will always manage to stay a little above bulk, and will probably climb towards $5 in the months and years after rotation.
Lands

Mana Confluence
1-2 Months: $10-$15
Rotation: $9-$12
Comparisons will be drawn to Cavern of Souls, but I think Nykthos is more appropriate. Cavern of Souls is used in Modern, Legacy, EDH, and Casual. Outside of Standard Mana Confluence is irrelevant to all but dredge players, so we’re not getting any real extra demand. Casual players hate paying life for mana, so there’s not much of a market there either. The price is basically completely driven by Standard. Those players will definitely want the land, but this isn’t an auto-four-of by any means. Aggro decks will max out but midrange and control lists aren’t going to be eager to pay that much life.
Nykthos sees mild play right now and hangs around at $7-8 so that’s probably Confluence’s floor. There will be considerably less copies of MC around, but Nykthos enjoys a bit of extra demand. Overall MC should hang out at a bit more than Nykthos if it sees comparable play. I’d say we’ll see this in the $10-$12 range for the most part, but it may take some time to get there. If it ends up overperforming we’re probably looking at it being $15+. If Thoughtseize can’t break $20, I don’t think MC can.


The Temples
1-2 Months: $5-$6
Rotation: $7-$8+
Most of the other Temples are in the $5-$6 range and there will be considerably more of those than there are of these. Lands nearly always rise at rotation and there’s no reason to expect ones with such a strong effect to behave any differently. Don’t hesitate to trade or buy your set now. You pretty much can’t lose. Hoard any you can get in trade because it’s likely enough that they break $10 that it’s totally worth risking them being $4-$5.