By now it’s no secret that I treat MTG investing very seriously. So seriously, in fact, that I compare the performance of my MTG portfolio loosely with that of the S&P 500. And why not? If I’m going to legitimately invest real dollars in original dual lands, shock lands, booster boxes, etc. then it only seems appropriate that I compare the return on these investments with that of other investment opportunities.
But my holistic approach to investing doesn’t stop here.
This week I want to dive into a more advanced economics topic out of the field of game theory by applying one of the most well-known truisms of game theory to our favorite MTG topic: buyouts. That’s right. I believe that we could potentially apply an advanced economics concept to understand something reactionary and emotional in the MTG Finance community. Think I’m crazy? Think it can’t be done? Well, allow me to at least try.
Nash Equilibrium
Before I jump into concept application, I need to establish a few assumptions first. These suppositions are not very far-fetched, so I don’t think you’ll have difficulty accepting my thesis because of these assumptions.
First, let’s assume that when a buyout of a certain card occurs, everyone attempting to purchase the card does so “simultaneously.” That is, when we’re ready to pull the trigger and make our purchase, we aren’t waiting for someone else to take their turn making a decision before us. We click the buttons as fast as we can to purchase the copies we want. And in the meantime, everyone else is doing roughly the same thing. In other words there is no turn taking or prescribed order.
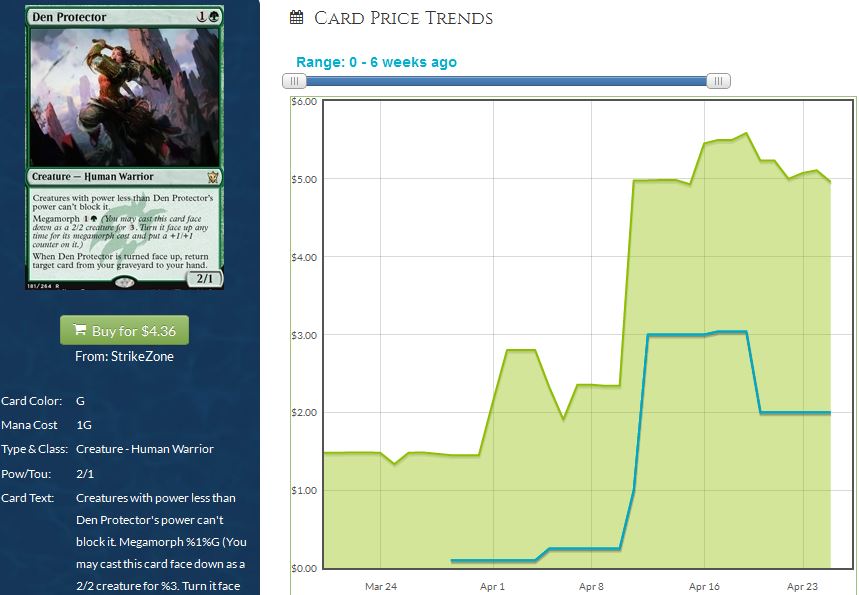
Second, we have to acknowledge buyouts occur in a non-cooperative manner. For example, when Den Protector spiked during the most recent Pro Tour, I wasn’t colluding with others in an attempt to obtain the market price I wanted. No strategy was involved in this regard. I rushed to eBay and TCGPlayer and picked up a bunch of copies as quickly as possible. I may have mentioned my actions on Twitter, but this communication was ex post facto. And even if I had cooperated with a friend, it’s not like the whole MTG community speculating on a card would ever work together – it’s an aggressive business we’re in!
With these assumptions in place, I will borrow Wikipedia’s eloquent definition of “Nash Equilibrium”:
“In game theory, the Nash equilibrium is a solution concept of a non-cooperative game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only their own strategy.”
John Nash was the famous economist who developed this theory and later earned a Nobel Prize for his work in the field. You may also recognize the name from the movie showcasing his genius and his struggles with schizophrenia, A Beautiful Mind.
 His Nash equilibrium concept describes motivations for people’s behavior when interacting non-cooperatively. (Aside: In game theory, any such interaction is referred to as a “game.” This is not comparable to playing a game of Magic – rather, the game I’m describing is the decision process of where we buy our cards and for how much during a buyout).
His Nash equilibrium concept describes motivations for people’s behavior when interacting non-cooperatively. (Aside: In game theory, any such interaction is referred to as a “game.” This is not comparable to playing a game of Magic – rather, the game I’m describing is the decision process of where we buy our cards and for how much during a buyout).
If we want to look at the definition of Nash equilibrium above, we can use specific terms to describe MTG buyouts. The first part of the definition describes the “solution,” or the actual outcome of everyone’s buyout decision (i.e. total copies purchased, where they were bought from, resulting price spike, etc). The second half of the definition is a bit more advanced. Essentially, the suggestion is that all parties involved know everyone else’s best strategy. In MTG buyout terms, we need to make one more assumption: the best action at the beginning of a buyout like Den Protector’s is to buy up copies at or near the starting price.
When a buyout happens due to legitimate demand, the card’s price jump is more likely to stick. Therefore, purchasing copies at or near the starting price during a buyout is definitely the best strategy – it makes you the most money! Everyone knows this, and everyone knows that everyone else is also eager to buy those $1.50 – $2.00 Den Protectors before they double or triple in price.
Thus, we say the Nash equilibrium of the buyout is that everyone buys up more and more copies of the card and the price catapults higher. This is the best strategy because those who bought at $1.50 – $2.00 can in turn sell their copies for profit.
Prisoner’s Dilemma
With Nash equilibrium established, I next need to define the crux of this week’s article: The Prisoner’s Dilemma. It’s this canonical example of game theory that I believe can be applied to MTG buyouts in a profitable way. But before jumping ahead, I first need to share another definition. Wikipedia defines the prisoner’s dilemma as “a game analyzed in game theory that shows why two purely “rational” individuals might not cooperate, even if it appears that it is in their best interests to do so.”
Originally framed by Merrill Flood and Melvin Dresher, the Prisoner’s Dilemma is a concept that can be applied to a diverse number of real-life interactions ranging from cola advertisements to nuclear stand-offs. My argument is that this sophisticated game theory dogma also applies to buyouts of Magic cards.
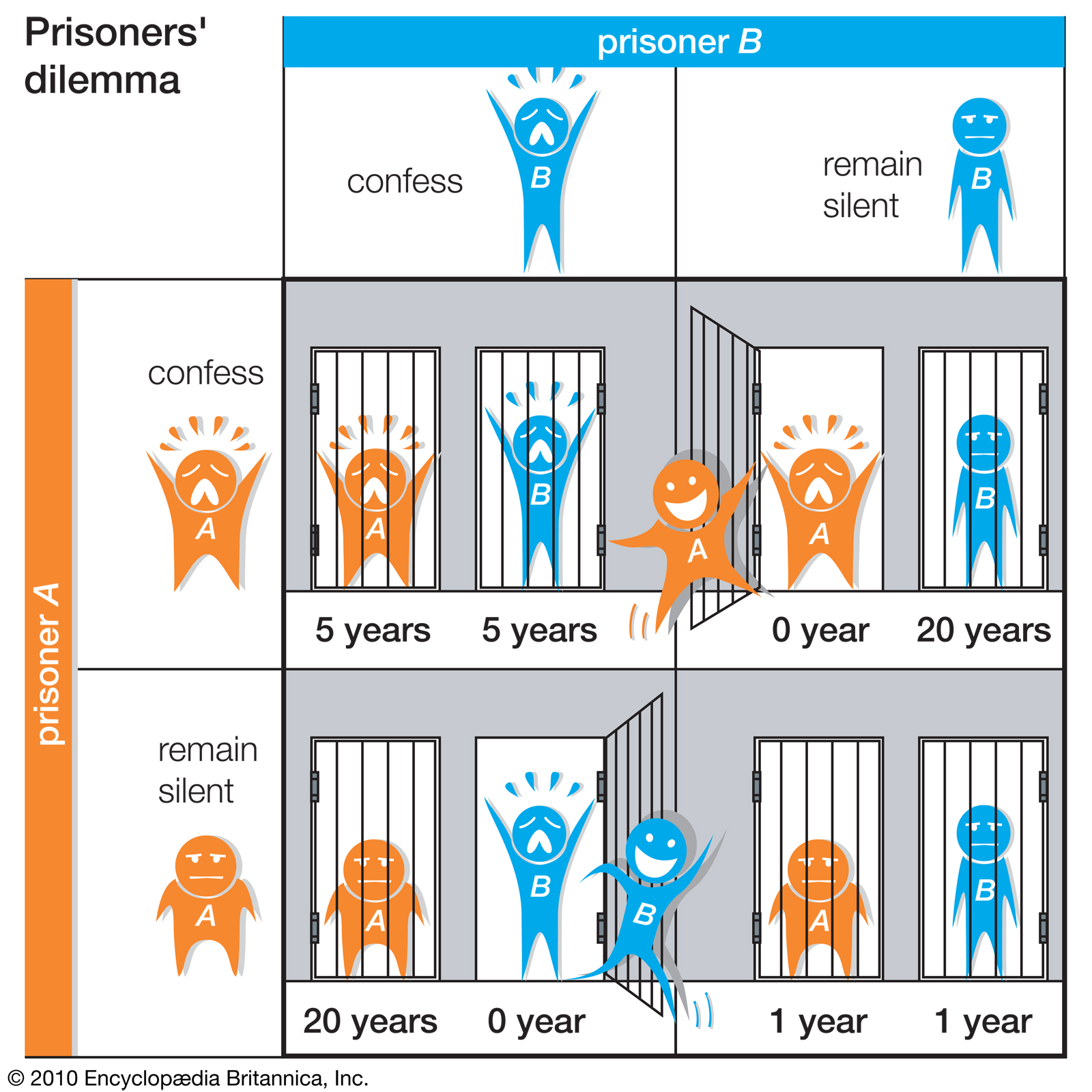
Explaining the Prisoner’s Dilemma is best done by example. The namesake explanation involves two strangers caught robbing a store together. They are brought to the police station where they are interrogated individually. The police do not have sufficient evidence to convict the prisoners of an armed robbery charge – only illegal possession of a weapon, which of course merits a much lighter sentence. So in an attempt to drive out a confession, they offer each prisoner separately the same deal: rat out your friend by confessing, and you will be rewarded with no imprisonment.
What’s the Nash equilibrium in this case? Put yourself in the shoes of one of the prisoners. If you assume your partner in crime is going to confess, then there are two possible outcomes: you don’t confess and take the fall, letting your partner walk freely while you suffer 20 years in prison for armed robbery and lack of cooperation with the police; OR you do confess, earning you and your partner a lighter, yet-still-strict sentence of 5 years in prison for cooperation. Given these two options, your best choice is to confess at least ensuring you avoid an unnecessarily long prison sentence.
Now what happens if you assume your partner is trustworthy and he is going to remain silent? Once again you have two choices: if you also remain silent, then the police cannot convict you of the armed robbery (there’s too little evidence) and you both receive a one-year sentence for illegal possession of a gun. On the other hand, if you confess, your partner would go to prison for 20 years while YOU get to walk away a free person. Given these two options, your best outcome is still to confess, since it means you don’t have to do any time in prison! That’s the best possible outcome for you!
The picture below depicts this interaction in a 2×2 grid.
No matter what you assume your partner will do, the best decision you can make is to confess. And that’s what happens – both prisoners confess netting themselves the five-year prison sentence.
The advanced part of this comes into play when we compare the actual outcome with the optimal outcome. It is undeniably ideal for both prisoners to remain silent – it nets them the least number of total years spent in prison! But because of the selfish assumptions of Nash equilibrium (i.e. there’s little emotional motivation for helping the other prisoner), both prisoners end up with a worse outcome because they do not cooperate.
How does this apply to Magic? I’ll argue there are two applications.
Application 1: Instead of dealing with prisoners and robberies, we’re dealing with purchasing a quantity of a Magic card at a particular price. We’re all faced with the same decision point during a buyout – do you pull the trigger quickly and grab copies or not? The more copies you buy, the more opportunity you have for profit.
In this game, buying up a ton of copies is equivalent to confessing and cooperation involves collusion. How do the outcomes look?
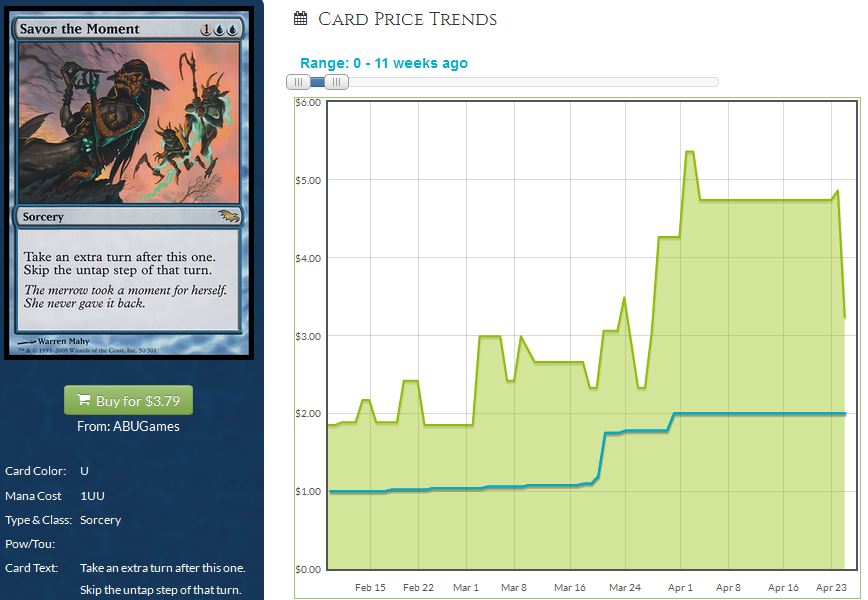
If everyone rushes out and purchases a ton of copies in an attempt to make bank, many participants in this game are stuck paying too much. As we’ve seen many times in the past, a buyout leads to a card’s spike followed by a race downward in price as people try to sell their copies for a quick buck. Savor the Moment is a recent example of this trend.
Notice how copies are scooped up aggressively starting in the $2.50 range in late March and ending in the $5.50 range, only to see a drop back down to around $3.25 most recently. When everyone decides to aggressively buy, the price jumps too high, too quickly. In these cases many people are left holding excess copies they are unable to sell for much profit because the higher price inevitably leads to a glut of supply as people try to cash in on the spike. Of course, those who don’t jump in with their hard-earned cash are in the worst shape of all. They own zero copies and they are stuck either paying a higher price or waiting for a drop that may never occur (usually the price ends up higher than the starting price but lower than the peak). No one wants to be in this scenario as it’s the worst possible outcome.
So what does everyone do? They all buy up as many copies as they can, sending the price higher and higher! Missing out on the “next big opportunity” is just too painful.
My argument is that this is another example of the Prisoner’s Dilemma. We all “defect” by purchasing a ton of copies while leaving those on the sidelines regretting their inaction. But this leads to a subsequent market glut and difficulty in liquidating copies at a profitable price. I’d argue the best possible outcome would be if the people who wanted copies most purchased the playset they need and those who don’t really want copies just ignore everything. Such cooperation would mean that the people who want copies would get their copies, but those who don’t simply stay away. The price may tick up a tiny bit, but there would definitely not be a huge spike. Then people who decide they don’t want their playset anymore could sell for a small profit and there would be no race to the bottom. And those who didn’t buy before aren’t faced with paying 50-100% more should they decide they want to obtain copies.
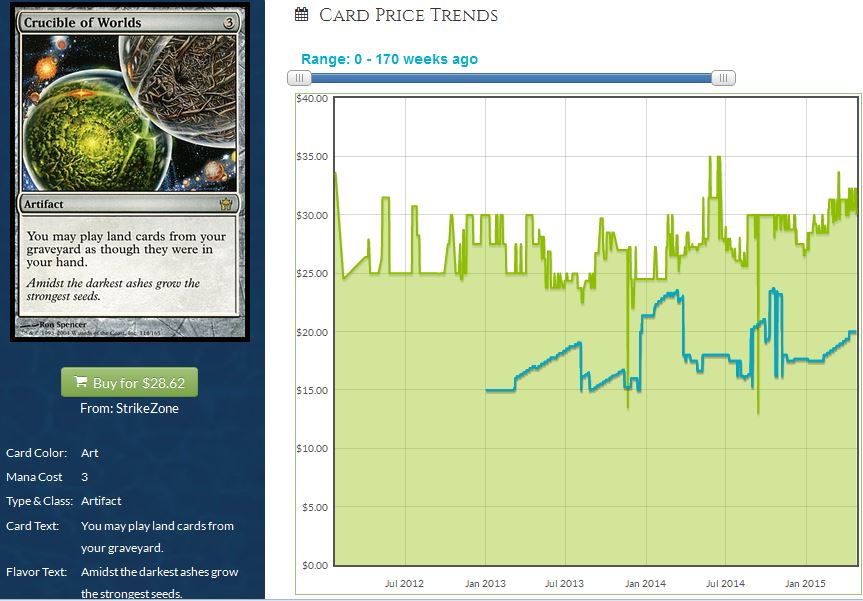
To me, this is the very definition of a healthy market. When a card increases or decreases in price it does so slowly and due to the natural shift in supply and demand. Crucible of Worlds is a great example of a card that has never been “bought out,” therefore leading to healthy price appreciation and no huge drops.
Wrapping It Up
So what’s the course of action here? Unfortunately, there is really little we can do to avoid the trap that is the Prisoner’s Dilemma. There’s a reason why both prisoners tend to confess, and Coke and Pepsi choose to advertise, and countries choose to invest in nuclear weapons, etc. etc. It’s not the optimal outcome for the entire population, but it is what inevitably happens thanks to Nash equilibrium.
I think the best thing we can do is at least make ourselves aware of this phenomenon before buying into the next spike. It would be naive of me to believe everyone can suddenly cooperate – it’s against human nature. But if we could at least communicate a little better as a community then perhaps we can soften the blow for those left holding the bag in a buyout. For example, when we make our purchases we could be more transparent with how many copies we’re buying and how much we are willing to pay for said copies. We could also make it public what our strategy is for selling – timeline and desired sell price.
Lastly, we could strengthen our relationships with others throughout the community. One thing Nash equilibrium always assumes is that everyone behaves rationally and in their best interest. Friendships and emotional attachment are disregarded. But of course these things DO exist in reality. By developing stronger ties with the rest of the MTG community, maybe we can all be slightly more sensitive to market manipulation. We’ll never eliminate price spikes altogether, but maybe we can help our friends avoid losing money by buying into the hype too late.
I’m out of words for this week’s column, but perhaps you’ve noticed something. I only shared one application, but I said there were two! In similar fashion to a “You Choose the Scare” R.L. Stein novel, I’ll pose the question to my readers: did you enjoy this topic enough that you’re curious to hear my second application as a Part 2 to this article? Or would you prefer I moved back to more traditional MTG Finance writing? Leave your opinion in the comments section, and we’ll let the majority rule!
Until then, thanks for reading!
…
Sig’s Quick Hits
- There’s another reason I used Crucible of Worlds as an example in my article. Nonfoil copies of the rare are completely sold out at Star City Games. Tenth Edition copies are sold out at $30.79 and Fifth Dawn copies are sold out at $32.35. If these don’t see reprint in Modern Masters 2015, there’s no reason they won’t continue to slowly chug higher.
- I honestly thought Bosium Strip was a forced buyout that would result in a subsequent price drop, just like my Savor the Moment example. But this has not been the case. Perhaps not enough copies of the card exist for the market to truly be “flooded” by eager speculators. In any event, SCG is sold out of the card at $4.89 and Channel Fireball currently has a buy price of $2.50!
- Another card that has healthily grown in price over time is Umezawa’s Jitte. The card has always been popular in various formats where it isn’t banned, but it’s never really in the spotlight. Star City Games has only 3 total copies in stock, with 0 NM copies at a $36.55 price tag.